Music Theory for Beginners 5: Key signatures, relative majors and relative minors

“Relative keys” is an important concept in music theory that’s able to unlock songwriting and improvisation potential. It grants you a deeper understanding of the relationship between the major and minor scales, and how to epitomise it in an arrangement. But before you start stringing notes together as effortlessly as Sir Elton John, you need a handle on the basics.

In the pentatonic scale lesson, we mentioned that while playing in a major key, you can deploy the major pentatonic scale or its relative minor equivalent. Relative minors and relative majors are, collectively as a concept, also known as “relative keys”. So just what is a relative key?

By the end of this lesson, you will:

• Understand the basics of ‘key signatures’
• Understand how key signatures inform the concept of relative keys
• Know how to derive relative keys using a related concept, the Circle of Fifths
• Know how to use relative keys in practice

Before you begin, it helps to take a glance at our introduction to scales, paying close attention to intervals, and our introduction to key changes. And if you haven’t internalised it already, you might also want to brush up on how a guitar’s fretboard works.

What is a key signature?

A key signature refers to the number of sharps (♯) or flats (♭) in a scale. Every major and minor scale has a specific key signature, such as “three sharps” or “two flats”.

A D major scale’s key signature, for instance, has two sharps, while an F minor scale’s key signature has four flats. A C major scale’s key signature, on the other hand, has no sharps and flats.

What is a relative key?

Relative keys are minor and major scales that share the same key signature; they have the same sharp, flat and natural notes – these constituent notes are known as “incidentals”. So, for instance, if two scales share a C♯, F♯ and G♯, they are said to have identical key signatures and, therefore, incidentals.

But does that make the scales identical? No. The differences lie in their tonics, which is a scale’s first and final notes – or its root notes. In other words, the scales start and end on different notes, lending each one a different feel. Just like how “1672” and “7216” have the same constituent numbers, yet are completely different.

We’ll revisit this further down, when we go through the practical application of relative keys. First, let’s take a look at how to derive them.

How it works in practice

As with much of music theory, there’s a shortcut. To find the relative minor of a major scale, all you need to do is count three semitones down from the latter’s root note.

Let’s give it a go. What is the relative minor of the A major scale?

• Counting down, A and G are one tone – or two semitones – apart
• And G to F♯ makes the third semitone

So, the A major scale’s relative minor is the F♯ minor scale. And this works the other way around, too: the A major scale is the relative major of the F♯ minor scale.

Try this exercise with a few scales, and don’t be afraid to venture into sharps and flats. The more familiar you are with this concept, the more confident you’ll be at improvising with key changes.

The Circle of Fifths

The Circle of Fifths, which, confusingly, is also dubbed the “Circle of Fourths”, is one of the cornerstones of Western music theory. Simply put, it’s a diagram that illustrates the relationship between all 12 ‘basic’ notes of Western music theory. Think of it as the Golden Ratio. It’s an abstract concept that’s largely based on mathematical ratios, but we’ll only be looking at its practical application here.

The Circle of Fifths is a handy tool that you can use to derive a scale’s relative key. We mentioned earlier that scales that share key signatures are related. The Circle of Fifths diagram is a cheat sheet that sorts the major and minor scales according to their key signatures:

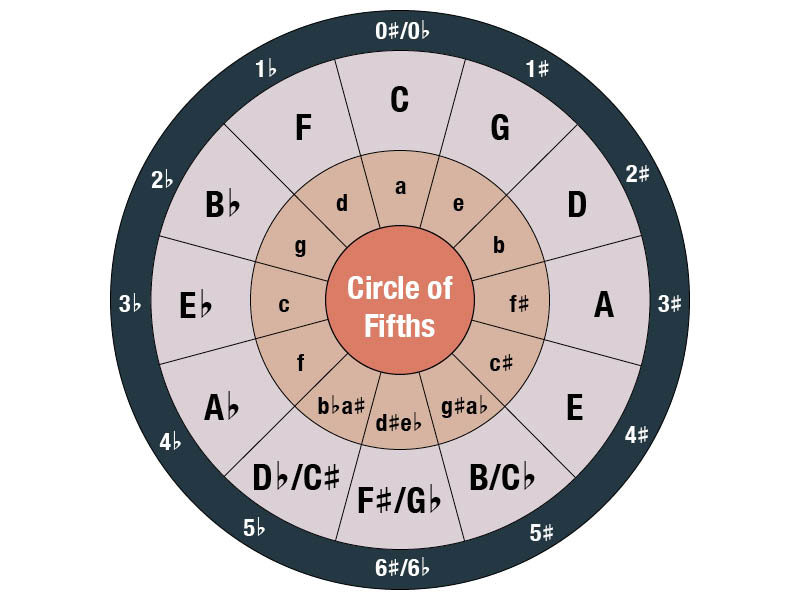
The chart is broken down like so:

• Inner ring: Minor Keys
• Middle ring: Major Key
• Outer ring: Key Signatures

So if you’re looking for B♭ major’s relative minor, simply locate the major scale on the middle ring. The corresponding key on the inner ring – which in this case is G minor – is its relative minor. The outer ring denotes their key signature, which is two flats (both scales have B♭ and E♭ notes).

How it works in theory

Here’s a simplified explainer on how the Circle of Fifths works:

The ‘fifths’ in the name refers to the perfect fifth, which we introduced in our lesson on basic chords. This type of fifth lies seven semitones above its root.

In the Circle of Fifths, every step in the clockwise direction represents a perfect fifth ‘movement.’ So for example, starting from the top, the distance between C major to G major is seven semitones – a perfect fifth.

And here’s why the diagram is also known as the “Circle of Fourths”: Every step in the anti-clockwise direction represents a perfect fourth ‘movement’, which is a distance of five semitones. Taking B♭ as a reference, a perfect fourth up would be E♭.

It’s important to note that no matter which direction you’re reading the chart, the perfect fourth or perfect fifth ‘movements’ are always going forwards from the root note, never back. As explained, a perfect fifth from C major is a G major (clockwise), but a perfect fourth from C major is an F major (anti-clockwise).

Applying relative keys to scales

Now that you know about relative keys, it’s time to get down to the fun stuff: applying them on your guitar.

Earlier, we mentioned that relative scales share the same incidentals but have different tonics. So while the notes of a major scale and its relative minor are identical, the scales start and resolve on different notes. Here’s the G major scale and its relative minor, an E minor scale, as an example:

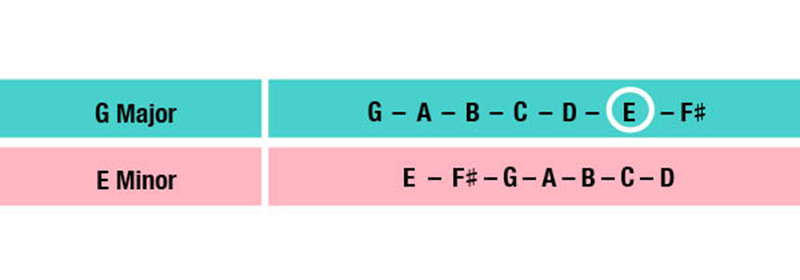
As you can see, the E minor scale starts on the sixth note of the G major scale. To give you a clearer picture of how this looks like on the fretboard, take a look at these two diagrams below.

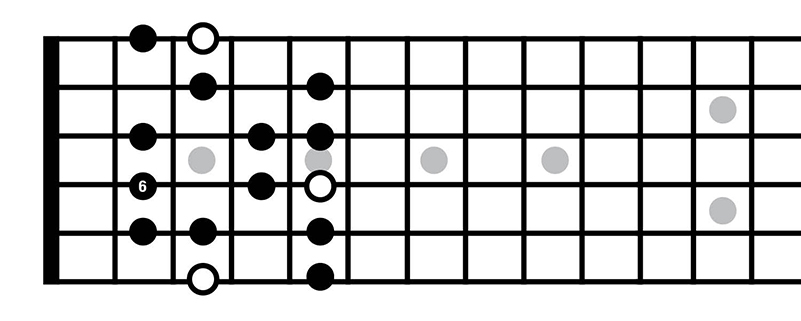
The first is a G major scale in the first position, with its sixth note, an E, marked out. The white dots represent G notes. This ought to be familiar to you:

The second diagram, however, illustrates how the E minor scale overlaps with its relative major. It begins on the sixth note of the G major scale and resolves after eight notes – or an octave. The notes that fall within the red rectangle is a box shape of the E minor scale:

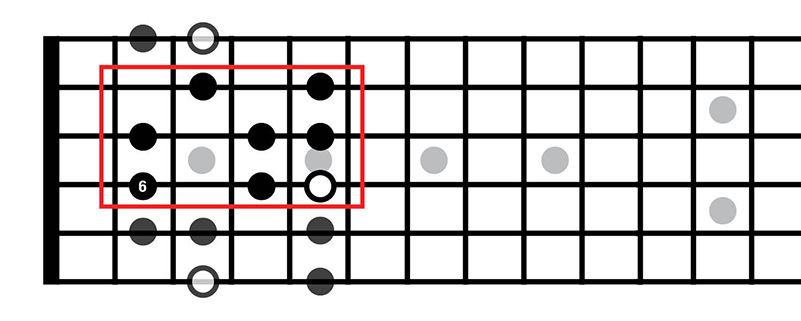
Try playing the G major scale in its entirety in the first position, and then play only the notes in the red rectangle. You’ll find that both evoke different emotions; the latter sounds more melancholic than the former. Yes, even though they comprise identical incidentals. To understand why requires knowledge of how the human brain processes successive pitches as relative to one another – but we’ll leave that to the neuroscientists.

Using relative keys in your band

So how do relative keys aid songwriting? They give you a sense of how to move between minor and major keys in fluid and musical ways. And, with enough practice flitting in and out of a scale and its relative key, they give you the confidence of writing lead lines over various chord progressions, especially those that have minor chords in a major key.

More importantly, it helps you understand the differences in tonality, which is imperative in picking the appropriate scale to deploy in a song. Of course, there’s no right or wrong way to do it. But if you play the Happy Birthday song in a minor key, it probably wouldn’t sound like a very happy birthday.

There’s much more to learn about tonality. But for now, keep practicing those scales, and see if you can apply the relative keys concept at your next jam session.

Editor’s note: A previous version of this article stated that the D major scale consists of one sharp. This error has since been amended.