Learn from your favourite guitar players here.
Related Tags
How to get better at guitar using the CAGED system (Part 3)
The midpoint of our series exploring the hidden depths of the CAGED system gets its teeth into the most common scale of all – the major scale.

Image: Getty Images
In Part 1 of this series about the CAGED System we discussed triads (three note chords) and in Part 2 the topic was pentatonic scales (five note scales). Now, let’s add another two notes to build the most common scale in western music: the major scale.
If you can play and also understand how this scale is constructed, you’re not far away from learning a whole lot of other stuff as well. A lot of music theory is derived from the major scale and I’ve mentioned it in the previous parts, but now we’re gonna dig a bit deeper and you’ll get an understanding of how you can find any interval in relationship to the major scale while visualizing the CAGED shapes.
So, the major scale contains seven notes within each octave. We have two half steps and five whole steps, this adds up to a total of 12 half steps from the root note up to the same note name, one octave higher. There are a few ways to look at the major scale from a theoretical standpoint – so check this out:

These seven notes are called natural notes as they’re neither sharpened nor flattened – they are also the white keys on a piano or keyboard. Any other major scale will contain one or several sharpened or flattened notes but the scale formula is always the same. As you can see above, the half steps in a C major scale occur between the 3rd and 4th note of the scale (E and F in this case) and between the 7th and 8th/1st note of the scale (B and C). Between all the other natural notes there are one note that can have two different names:
- The note between C and D can be considered either a sharpened C (C♯) or a flattened D (D♭)
- The note between D and E can be considered either a sharpened D (D♯) or a flattened E (E♭)
- The note between F and G can be considered either a sharpened F (F♯) or a flattened G (G♭)
- The note between G and A can be considered either a sharpened G (G♯) or a flattened A (A♭)
- The note between A and B can be considered either a sharpened A (A♯) or a flattened B (B♭)
When building a major scale we need a note derived from each of the natural notes, all represented once. No more, no less. However, they can be sharpened or flattened. We can’t have both D♭ and D in the same scale for example. We also don’t want to mix ♯’s and ♭’s. With this in mind, let’s build a major scale starting from A♭ for example:
- A♭ is the root
- B♭ is the major 2nd (this won’t be called A♯ since we already have the root note derived from the natural A)
- C is the major 3rd
- D♭ is the perfect 4th (this won’t be called C♯ since we already have the C as our major 3rd)
- E♭ is the perfect 5th (this won’t be called D♯ since we already have the perfect 4th derived from the natural D)
- F is the major 6th
- G is the major 7th
- A♭ takes us back to the octave/root note.
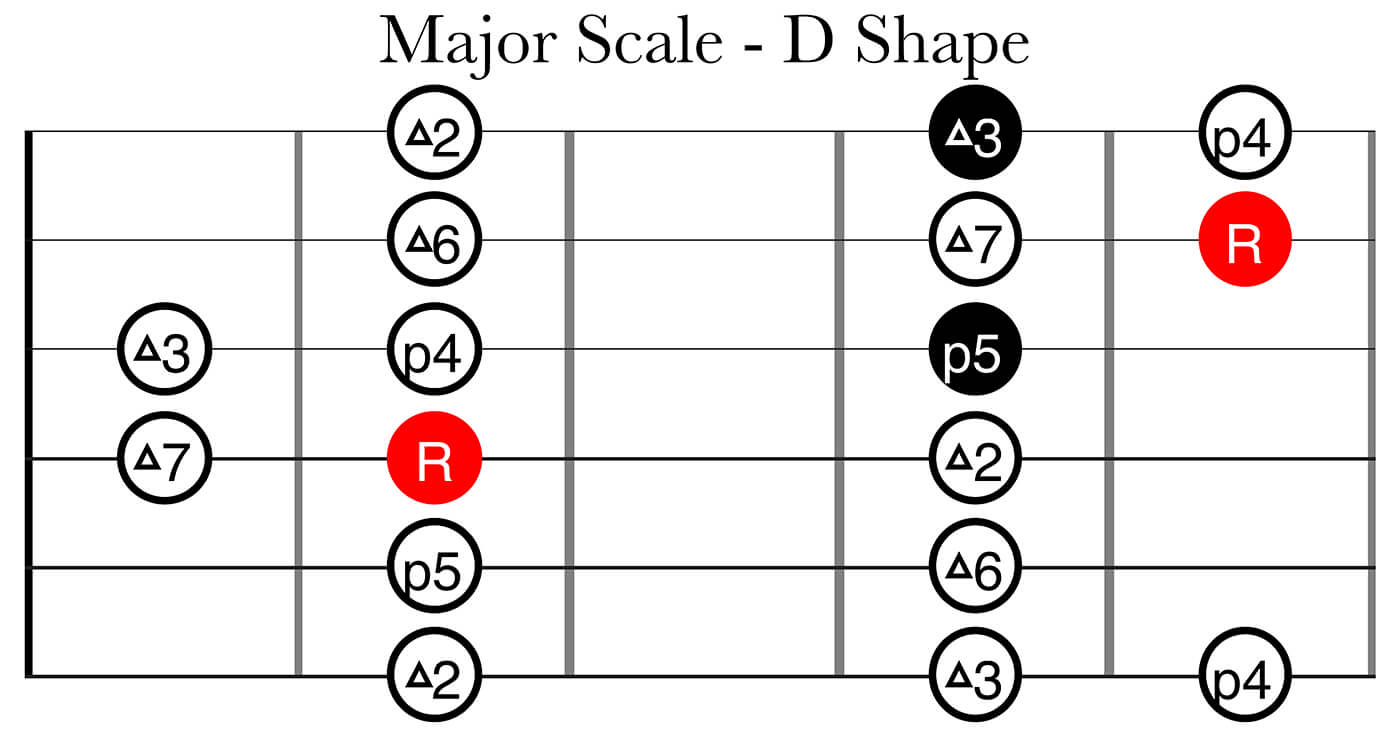
Knowing this, you should be able to build all the 12 major scales and actually understand the relationships between all the notes and not only memorize a certain fingering pattern. Here are the major scale in all the five CAGED shapes:
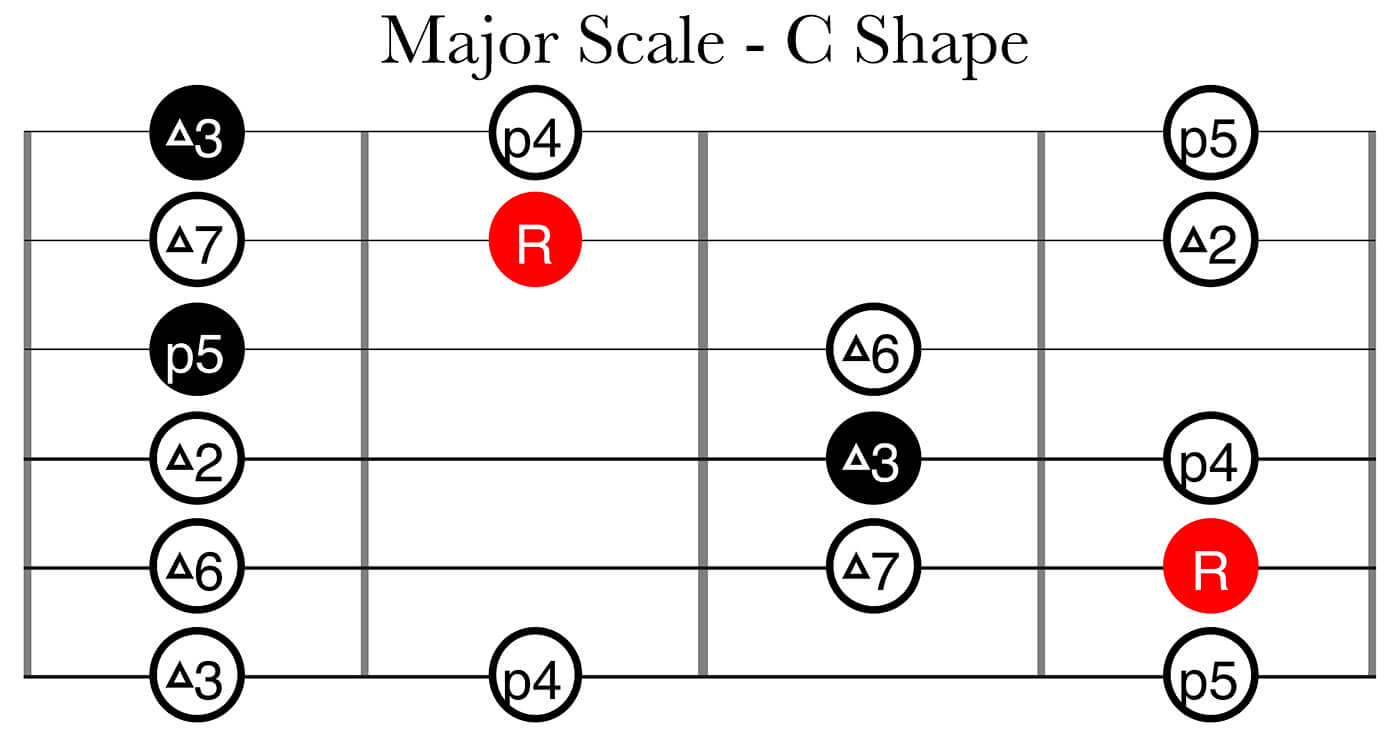
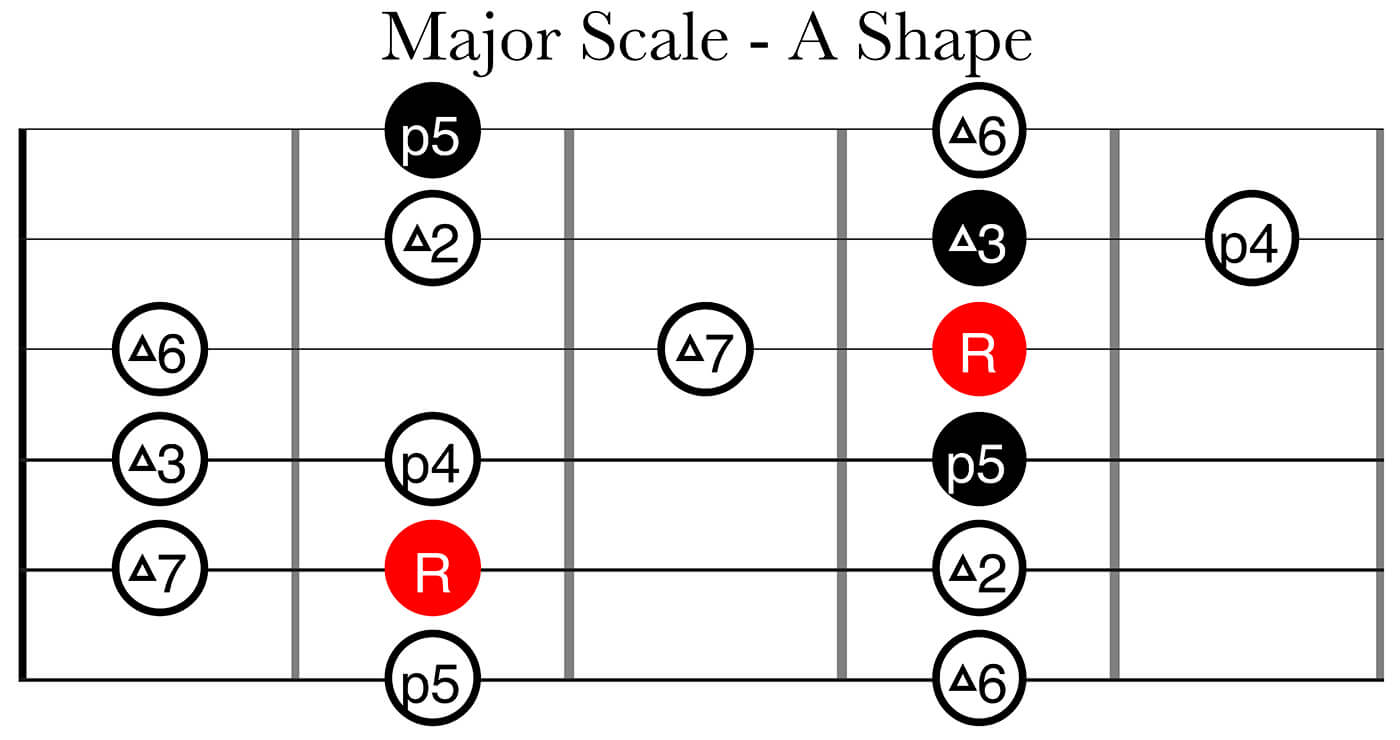
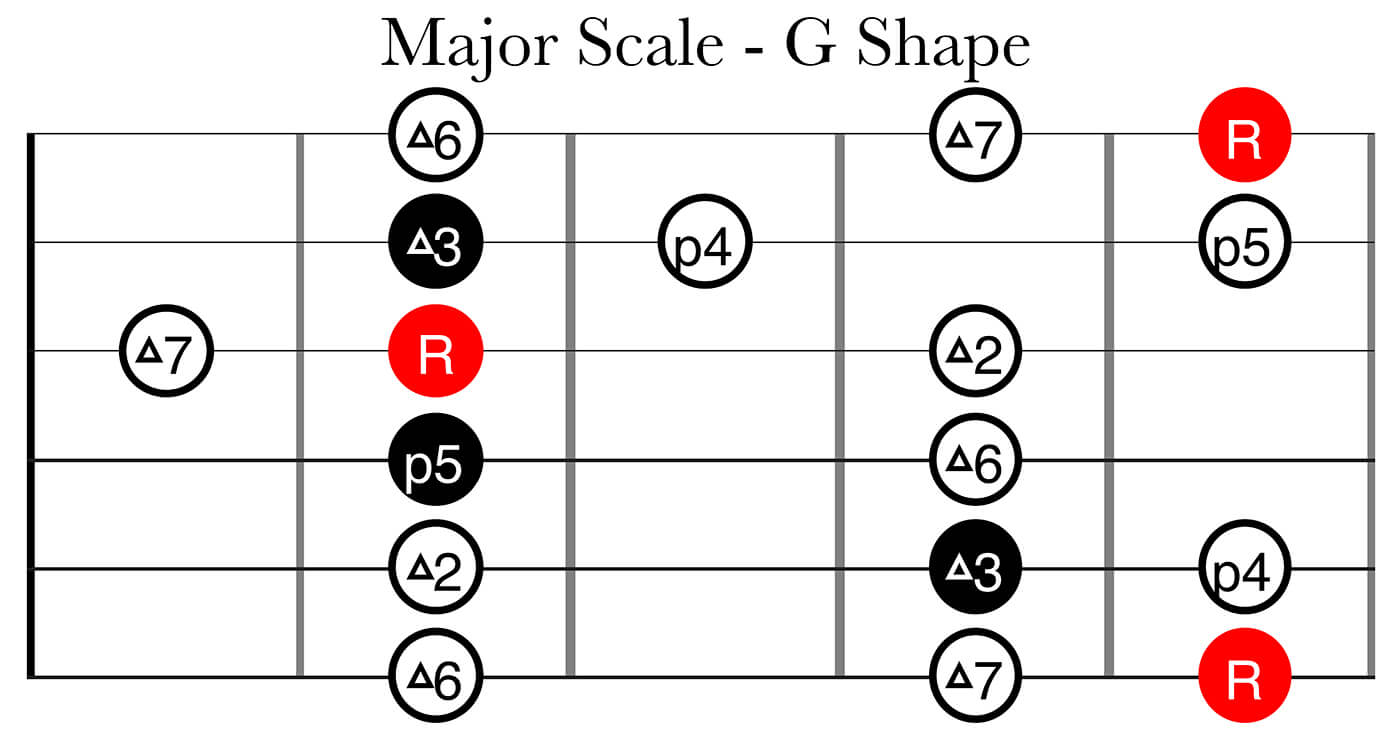
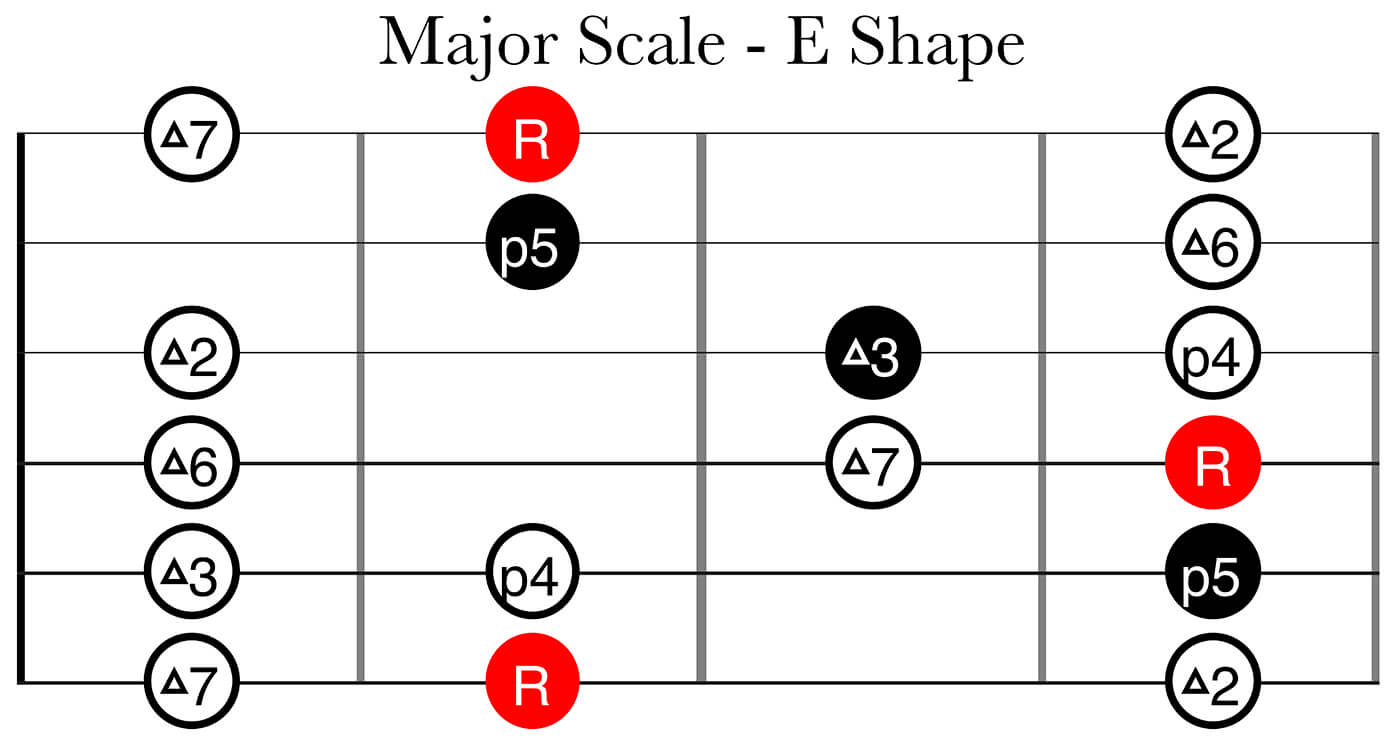
The following diagrams shows how we start with the template of just the triad, just one note per string and three notes per octave – the root, major 3rd and perfect 5th. Then we add two more notes per octave, the major 2nd and major 6th, to get the five note major pentatonic scale – note that there are still no half steps. Finally we add the perfect 4th and the major 7th, this is our full major scale – I outlined these two notes as triangles so you can see clearly where the half steps occur. Where the half steps are placed greatly impacts the sound of the scale, I’ll go into greater detail regarding this in a later part of this article series.
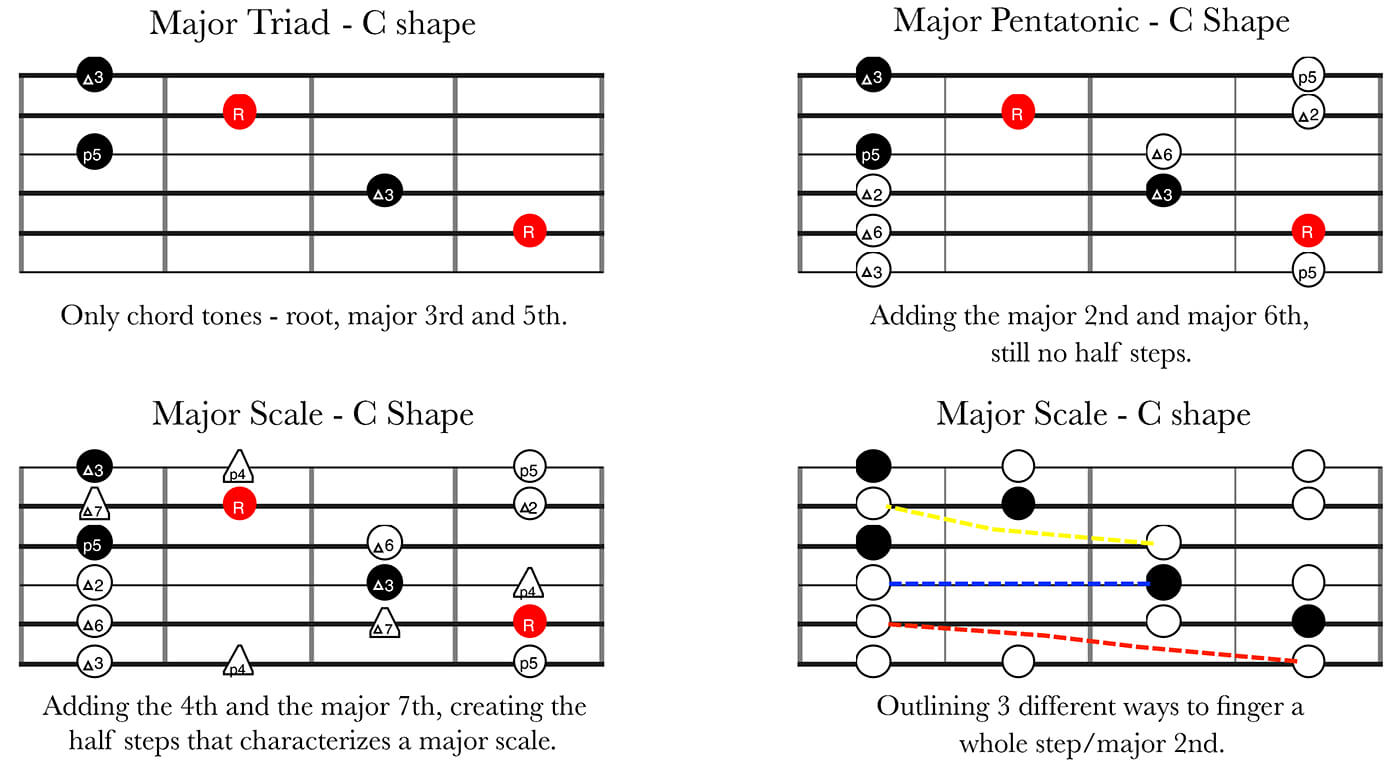
In the lower right of these diagrams I’m highlighting three different ways to finger a major 2nd/whole step:
- Dotted yellow line: a major 2nd/whole step always looks like this between the G/B strings
- Dotted blue line: a major 2nd/whole step always looks like this when played on the same string
- Dotted red line: a major 2nd/whole step always looks like this between the E/A, A/D, D/G and B/E adjacent string sets
When using the CAGED system it’s rare that you finger a minor 2nd/half step interval on different strings. Hopefully though, by now you will likely understand that: as long as you know what a major 2nd/whole step looks like, you can just lower the higher note one fret and the interval will turn into a minor 2nd/half step interval.
Think chromatic
Now, let’s go beyond the major scale and figure out all the rest of the intervals within an octave. One octave contains twelve notes in total and a major scale, as you know by now, is built from seven of these notes in a sequence of whole steps and half steps. That means we have five gaps (where the whole steps occur) that we could potentially fill in with other notes, this would create the 12-note chromatic scale – that contains only a series of half steps. This is similar to what we did earlier in this lesson but instead of using note names now we focus on the intervals, so it’s not specific to any certain key.
- We can add a note between the root and the major 2nd, we call that a minor 2nd or ♭2.
- We can add a note between the major 2nd and the major 3rd, we call that a minor 3rd or ♭3.
- We can add a note between the perfect 4th and the perfect 5th, we call that either an augmented 4th or ♯4. Alternatively diminished 5th or ♭5.
- We can add a note between the perfect 5th and the major 6th, we call that a minor 6th or b6. Alternatively augmented 5th or ♯5.
- We can add a note between the major 6th and the major 7th, we call that a minor 7th or ♭7.
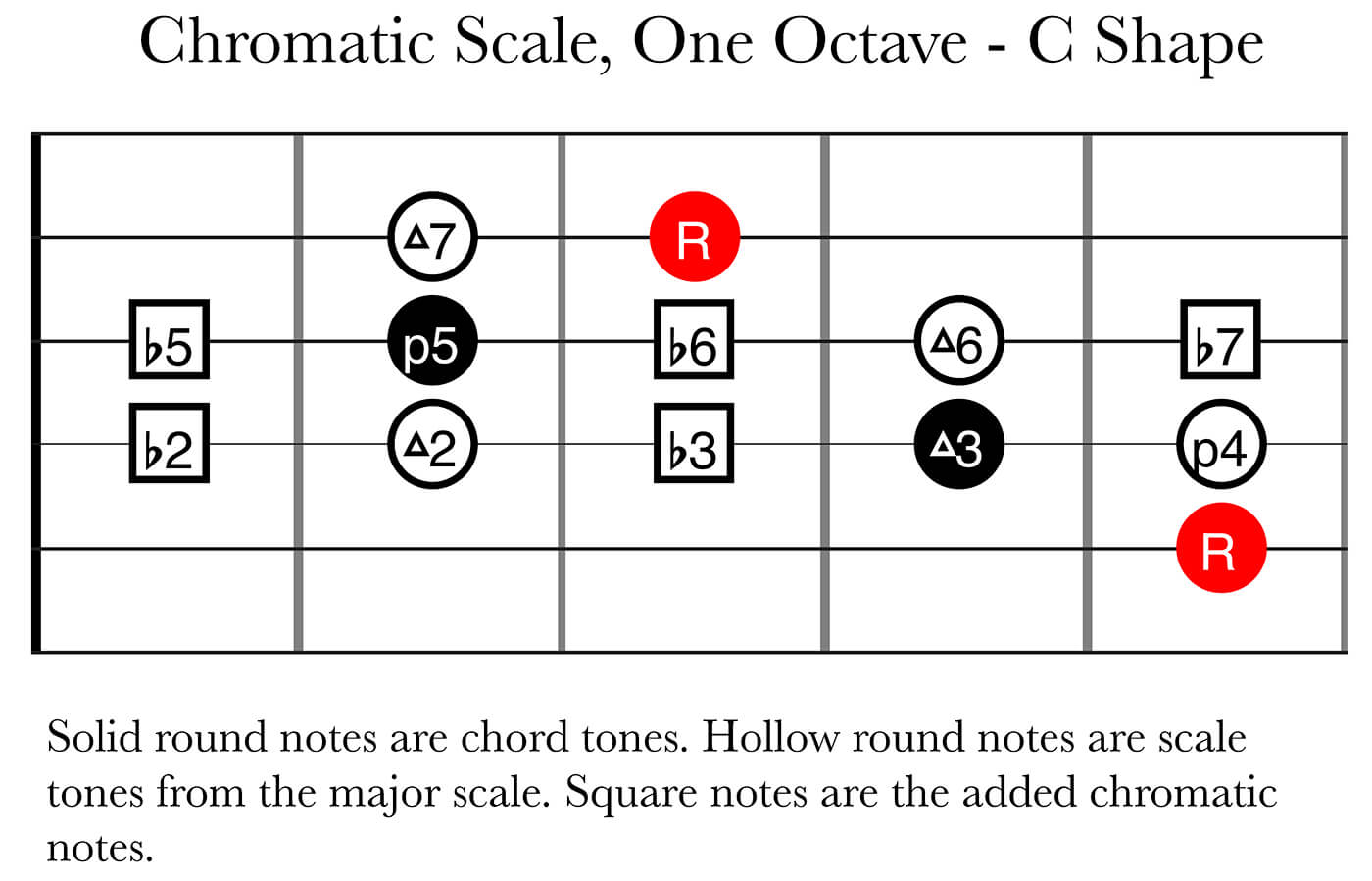

Now study these two diagrams of the chromatic scale in the C and E shape. I haven’t included all the five shapes on purpose because I want you work on your ability to draw connections between the different shapes. Remember that the C and G shapes are closely connected, and that the A, E and D shapes are equally connected. I’ve explained this in earlier articles in this series, so go back and check those out if you are unsure of how this works. I want you to follow this routine when studying these intervals.
Question: How can I finger a minor 6th according to these diagrams?
Answer: The C shape shows one way to do it, between the A and G strings. The E shape show two ways of doing it, between the low E and A strings, as well as between the D and B strings.
Follow up question: Does the same fingerings apply to any other string sets?
Answer: Yes, you can use the same fingering as between the low E and A strings but move it to the A and D strings, or D and G strings. This is still a minor 6th and can be found within the A shape and the D shape, respectively. You can also reuse the fingering of a minor 6th between the D and B strings and move it to the G and high E strings.
One important thing is to realize the difference between intervals and scale degrees. Here are a few examples in the key of G:
- The G note is the root and the E note is the major 6th – they are a major 6th apart from each other IF the G played lower. If the E would be played lower and then the G added on top, they would be a minor 3rd apart. Both versions contain the same harmonic content over a G chord but still have a slightly different flavor. This is called inverted intervals and is a super useful thing to know about, it basically means shifting the octave of one of the notes to create either a wider or tighter interval.
- The C note is the perfect 4th and the A note is the major 2nd (or major 9th when played an octave up) – they are also a major 6th apart but will create a very different sound over a G chord.
The interval name just describe the distance between two notes, no matter what context you’re in. However, the scale degrees tells the relationship to the key or root note. Both are important.
This diagram shows the major 6th intervals found within the major scale in the G shape. If you take the higher of each pair of notes and lower them an octave, you’ll find all the minor 3rds within the major scale. I highly encourage you to explore the CAGED shapes in this way, it really helped me to unlock the fretboard.
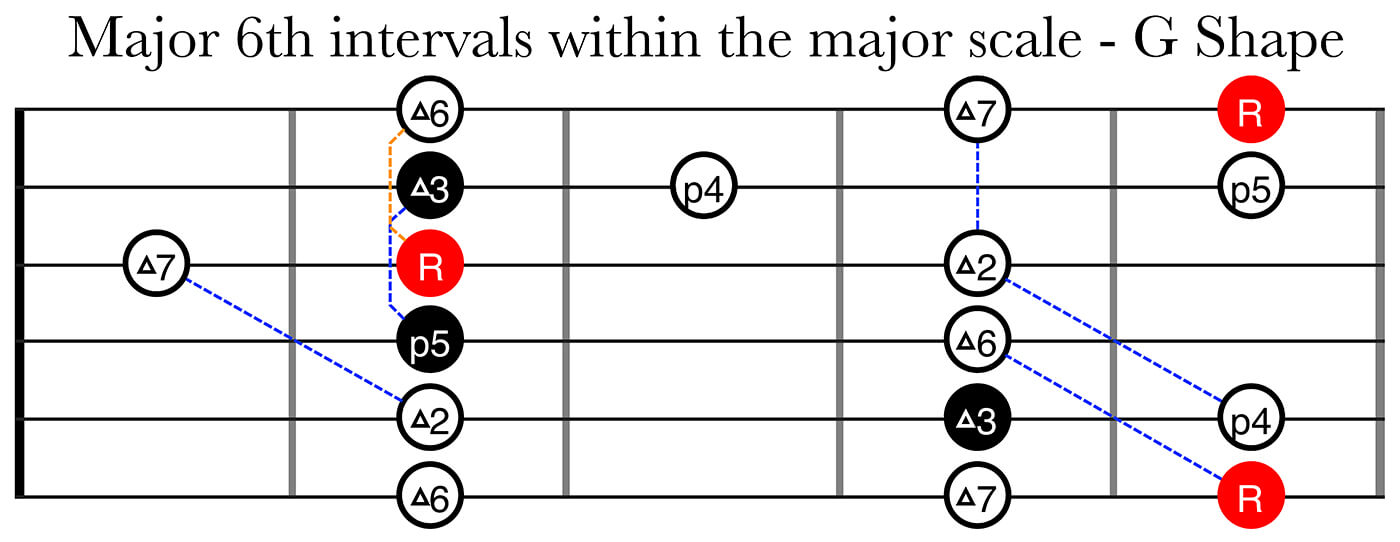
This is not easy and it will take some time to get a grasp on, but a lot of the patterns are moveable and when you start seeing connections and similarities between the different shapes you’ll get a MUCH deeper understanding of the fretboard and how’s it connected. Good fretboard visualization is incredibly important to become freer on your instrument and communicate the musical ideas you hear in your head.
